In the third and last part of this special we will talk about the economic thickness of thermal insulation.
by Eng. Arcadio Velásquez*
Have you ever wondered what is the right thickness to reduce heat loss/gain? Is it true that the higher the thermal insulation, the better the performance?
A short and quick answer to that question is "yes, it is." That's the first thing that usually comes to mind. Why not? Is that correct?
The thickness of thermal insulation can be calculated based on two different requirements in the case of cooling systems: one is to prevent condensation and the other is to reduce the density of heat transfer (heat loss/gain). The basic calculations are defined in ISO 12241.
To prevent condensation in any cooling system, only the minimum insulation thickness is needed, which is a value that depends on the environmental conditions of the surrounding air (temperature and humidity), if these conditions change, then the minimum insulation thickness to prevent condensation will be different. How different? For that, we must refer to ISO 12241, Clause 4.3 Prevention of surface condensation.
Minimum thickness to prevent condensation
Calculating the minimum thickness to avoid surface condensation on pipes is a very easy task, according to ISO 12241 we need to calculate the thickness parameter C'. There are two equations for this: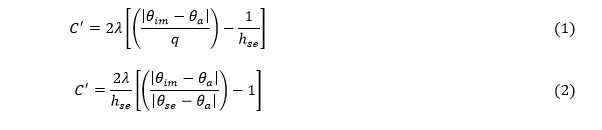
Where
θ_im: Medium temperature
θ_a: Room temperature
θ_se: External surface temperature
λ: Thermal conductivity at medium temperature
q: Heat flux density
h_se: Surface coefficient of heat transfer
Equation (1) works with the density of the heat flux while equation (2) works with the dew formation temperature.
Let's make an example considering the dew formation temperature, the following example is to explain the minimum thickness to avoid condensation in steel pipe.
θ_im: 10 degrees Celsius
θ_a: 20 degrees Celsius
D: 0.108 m (carbon steel pipe)
λ: 0.039 W/(m.K)
φ: 85%
h_se: 5.4 W/(m2. K)
Step 1- Dew formation temperature.
According to ISO 12241, Table 4: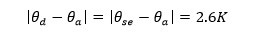
Step 2 – Calculation of parameter C'.
Using equation (2) and an elastomer as insulator, the average temperature is 13.7 ⁰C.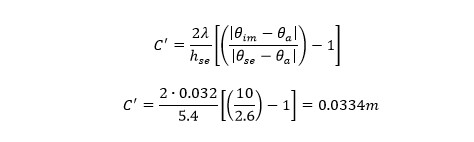
When the parameter C' is 0.0334m, with the help of figure 9 of ISO 12241*, the minimum thickness to avoid condensation is approximately 13.00mm.
Surface condensation depends not only on parameters affecting the surface temperature, but also on the relative humidity of the surrounding air, which very often cannot be accurately declared by the user.
The higher the relative humidity, the more fluctuations in humidity or surface temperatures increase the risk of surface condensation. Unless other data are available, assumptions such as Table 3* are necessary to calculate the insulation thickness needed to prevent dew formation in pipes. Using Equation (48)*, the insulation thickness needed to prevent dew formation can be obtained by iterative techniques. The permissible temperature difference, expressed in Kelvin, between the surface and the ambient air for different humidity relative to the onset of dew formation is given in Table 4*.
Optimal thickness to reduce heat flux density (heat loss/gain): Economic thickness is the thickness of a thermal insulation material that minimizes the total cost (investment and running costs) over a specified period - balances the cost of interest payments incurred to insulate the system against the cost of energy saved as a consequence.
The isolation of any system means an investment. Therefore, the most important factor in any insulation system is to analyze thermal insulation with respect to cost. The effectiveness of isolation follows the law of diminishing returns. Therefore, there is a definite economic limit to the amount of insulation, which is justified. A higher thickness is not economical and cannot be recovered through a low thermal performance improvement. This limiting value is called the economic thickness of thermal insulation.
Let's look at an example, considering the same conditions described in the previous example: we used 4 different thicknesses of an elastomer (NBR) with thermal conductivity 0.033 W/mK at 23 degrees Celsius as the average study temperature - from the minimum thickness to avoid condensation, which was 13 mm (1/2"), then gradually increase the thickness to 25 (1"), 50 (2") and 75 mm (3"). See Figure 1 and 2 for results.
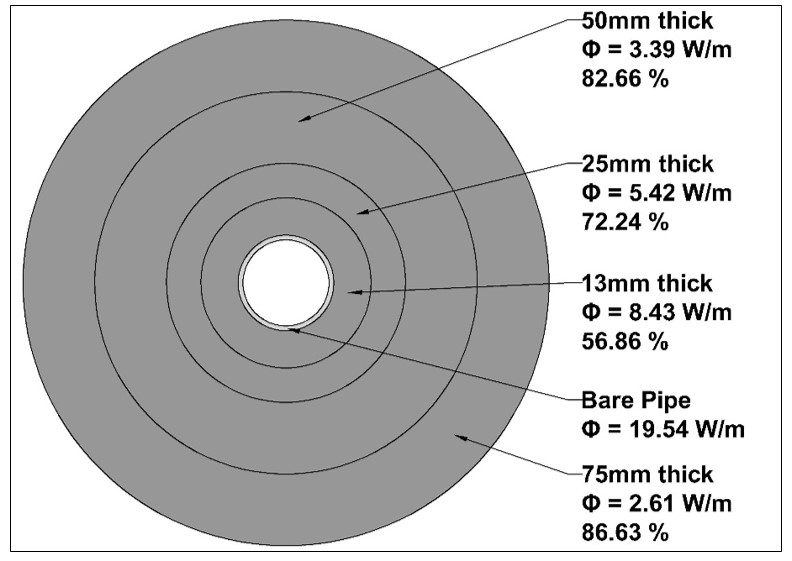
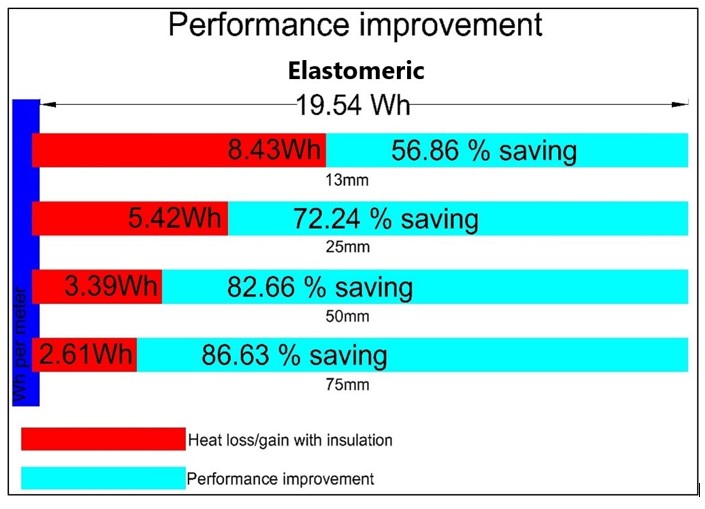
How to calculate the economic thickness?
There are two methods for calculating economic thickness:
(1) Graphical method: After collecting all the data, including the initial investment, insulation cost, operation and maintenance, energy/fuel cost, a graph will be arranged as shown in figure 3.
Computerized calculations: there are several computer programs designed to calculate the economic thickness of thermal insulation.
To calculate the economic thickness, we need to organize the following information:
- Pipe surface temperature without insulation.
- Dimensions such as diameter, length and surface area of the pipe section under consideration.
- Average ambient temperature.
- Since we are doing the calculations for the commercially available insulation thickness, some trial and error calculations will be required to decide the surface temperature after placing the insulation.
- Select an insulation material, with known thermal conductivity values in the average insulation temperature range.
- Calculate thermal resistance and insulation thickness.
- Estimate the surface area of the pipe with different insulation thicknesses and calculate the total heat loss from the surfaces.
- Estimate the cost of energy losses.
- Calculate the net present value of future energy costs over an insulation lifetime of typically 5 years to 10 years – depending on the insulating material.
- Calculate the total cost of putting insulation in the pipe (material + labor cost)
- Calculate the total cost of energy and insulation costs for 3 situations.
- The insulation thickness corresponding to the lowest total cost will be the economic thickness.
The following graph (Figure 3) has been made using Aero-calc to determine heat loss/gain based on the example above. Taking into account the total cost of the insulation and its installation, for this particular case the economic thickness is between 25mm (1") to 32mm (1-1/4"), it is recommended to select the following standard size. Result in table 1.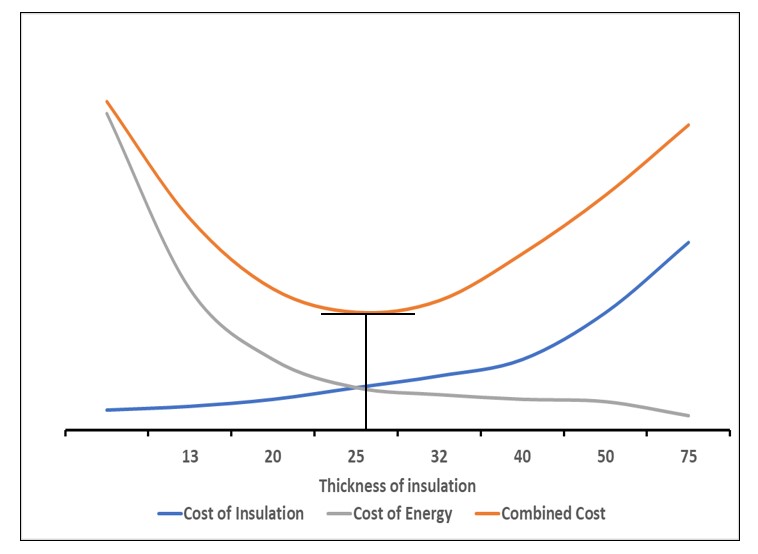
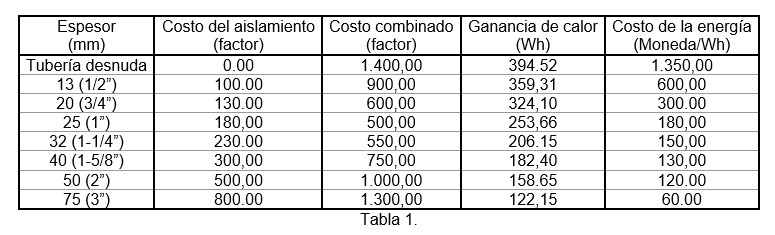
Table 1 contains calculations of the cost of insulation and electrical energy – if we focus on behavior, as we increase the thickness increases the combined cost but energy savings are not improved on a considerable scale. We can conclude that the solution is not to randomly choose the largest isolation without first doing a detailed study.
What are the differences between the minimum thickness to avoid surface condensation and the economical thickness? The minimum thickness will prevent the formation of dew; However, the amount of energy savings will be so low that it can lead to economic losses for the end user - the longer the material is used, the more money the end user will lose - The solution is not to select a larger thickness before doing a detailed analysis. That analysis is the economic thickness, which will help balance the cost of investment and operation along with the return on investment based on energy savings.
Advantages of economical thickness
The benefits of economic thickness will vary depending on the application and method of financial evaluation. One of the simplest methods of financial evaluation is payback analysis, where costs are compared to savings and the result is expressed in terms of payback period.
* Helps estimate return on investment (ROI): A properly designed and installed insulation system provides excellent return on investment and rapid payback through cost savings. Insulation is a low-risk investment because savings and recovery can be predicted with a high degree of accuracy.
Insulation is one of the few technologies where payback is considered more than acceptable compared to many other equipment purchases or maintenance. If the isolated system is well maintained, the investment savings continue over the life of the facility. In fact, it costs more not to insulate properly. Often, insulation is paid for with the maintenance budget and then reduces the operating budget over the life of the system.
* Helps control temperature and process stability: Insulation can be used to maintain process temperatures in different industries, including food and beverage, pharmaceutical, oil and gas, and even in buildings and constructions. In addition, depending on the application, it can provide security to users by maintaining an adequate temperature of the surfaces of the systems.
What else can economic thickness offer?
Protect the environment by reducing CO2 emissions.
Lower energy consumption means less pollution. Thermal insulation reduces energy consumption, which means less fossil fuel is burned to produce that energy. This, in turn, decreases the number of polluting gases such as carbon dioxide and sulfur dioxide emitted into the atmosphere. Because carbon dioxide is one of the main greenhouse gases contributing to global warming, insulation plays an important role in protecting the environment.
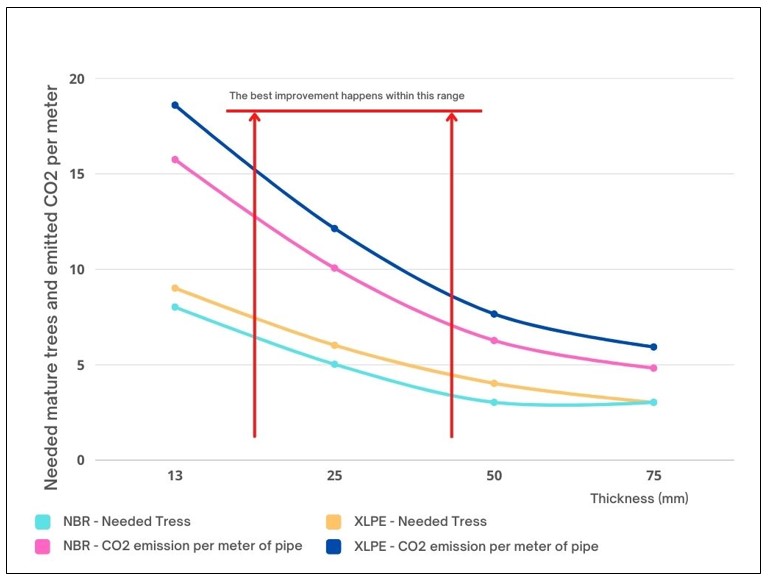
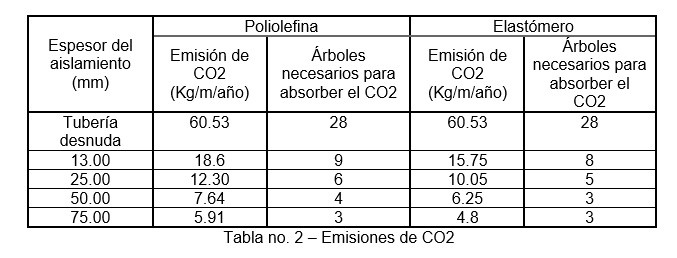
Taking into account the previous example, we calculate the CO2 emission for XLPE (Polyolefin) and NBR (elastomer) considering 4 thicknesses, in addition to the trees necessary to absorb the CO2 emitted. Using a graph, it is easy to recognize that the best improvement in terms of CO2 reduction and the number of trees needed occurs around the economic thickness as planted in the graph below:
Below are the results of the analysis on CO2 emissions, considering pipe of 10m in length.
 * Arcadio J. Velásquez | Mechanical Engineer.
* Arcadio J. Velásquez | Mechanical Engineer.
Sr. Technical Marketing Engineer - Hira Industries LLC.
Thermal Insulation Specialist
Dubai, United Arab Emirates.
[email protected]















